Từ cây nhị phân tới cây đỏ đen
Tác giả: Nguyễn Bá Ngọc
1. Các khái niệm và thao tác cơ bản 1
2.1. Tìm phần tử trong cây nhị phân tìm kiếm 5
2.2. Thêm phần tử vào cây nhị phân tìm kiếm 6
2.3. Xóa phần tử khỏi cây nhị phân tìm kiếm 7
3.1. Thêm phần tử vào cây đỏ đen 11
3.2. Xóa phần tử khỏi cây đỏ đen 13
Cây nhị phân bao gồm 1 tập nút trong đó có 1 nút đầu tiên được gọi là gốc, các nút còn lại được phân chia thành 2 tập con, mỗi tập con lại tiếp tục được tổ chức như 1 cây nhị phân và tương ứng là các nhánh trái và nhánh phải của nút gốc.
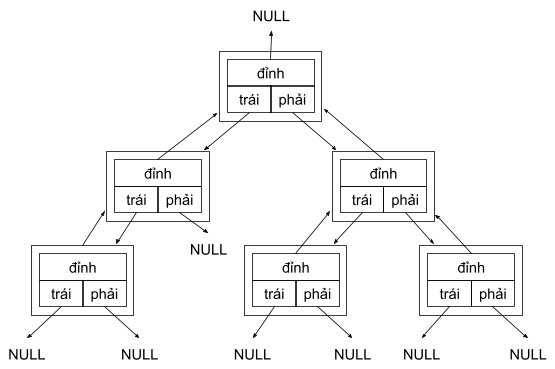
Từ cây mượn hình tượng cây trong tự nhiên - có 1 gốc và từ đó phát triển vươn cành, chia nhánh. Tuy nhiên trong các hình vẽ cây nhị phân thường được biểu diễn phát triển từ trên xuống dưới, gốc ở trên cùng, các nhánh ở phía dưới. Xuất phát từ gốc có thể đi đến tất cả các nút còn lại trong cây. Từ nhị phân có nghĩa là mỗi nút trong cây có 2 nhánh. Tuy nhiên trong triển khai thực tế bên cạnh 2 liên kết tới các nhánh mỗi nút có thể được bổ xung 1 liên kết lên trên, về phía gốc, tới nút duy nhất mà nó có thể là nút dưới trái hoặc nút dưới phải phải, được gọi là nút đỉnh[1]. Trường hợp đặc biệt chỉ có gốc cây không có nút đỉnh tương ứng. Bổ xung liên kết tới đỉnh làm tăng tính linh hoạt trong duyệt các phần tử của cây, xuất phát từ 1 nút bất kỳ trong cây có thể đi tới 1 nút bất kỳ khác, tuy nhiên về lý thuyết mỗi nút vẫn được coi là chỉ có 2 nhánh trái và phải. Nếu chỉ duy trì 2 liên kết tới các nhánh trái và nhánh phải thì chỉ có thể di chuyển từ gốc tới các phần tử khác trong cây chứ không thể di chuyển theo chiều ngược lại. Cây nhị phân với liên kết tới nút đỉnh được minh họa trong Hình 1.
Hình 1. Sơ đồ liên kết của cây nhị phân
Trong Hình 1 các nút được biểu diễn bằng các hình chữ nhật được gọi là các nút trong. Các nút trong có thể chứa dữ liệu. Giá trị NULL đánh dấu điểm kết thúc của đường đi. Các giá trị NULL của các liên kết trái và liên kết phải của các nút trong được gọi là các nút lá. Còn 1 giá trị NULL duy nhất là đỉnh của gốc cây, giá trị NULL đó không phải nút lá.
Độ cao của 1 nút trong cây nhị phân là số lượng cạnh trong đường đi đơn giản dài nhất từ nút đó tới nút lá. Đường đi đơn giản nghĩa là không chứa chu trình, chỉ đi theo các liên kết trái hoặc liên kết phải. Độ cao của 1 cây nhị phân được hiểu là độ cao của nút gốc của nó. Có thể định nghĩa độ cao theo cách tương đương là số lượng nút trên đường đi đơn giản tới lá nhưng không đếm nút bắt đầu.
Cây nhị phân cân bằng theo chiều cao là cây nhị phân thỏa mãn điều kiện với 1 nút trong bất kỳ thì chiều cao nhánh trái và chiều cao nhánh phải của nó lệch nhau không quá 1. Trong thực tế còn có hình thức cân bằng khác, ví dụ cân bằng theo trọng số, tuy nhiên bài viết này chỉ sử dụng khái niệm cân bằng theo chiều cao, vì vậy nếu không có lưu ý gì thêm thì khái niệm cây nhị phân cân bằng được mặc định cân bằng theo chiều cao.
Dựa trên cấu trúc liên kết có thể thấy cây nhị phân trong Hình 1 là 1 cây nhị phân cân bằng, độ cao của cây = 3, các nhánh trái và nhánh phải của gốc cũng là các cây nhị phân cân bằng.
Các diễn đạt thay thế nút x bằng nút y ngầm định các nội dung sau: Trong các liên kết với nút trên của nút x; không thay đổi các liên kết trái và liên kết phải của cả nút cũ và nút mới; nếu x đang là gốc của cây thì đỉnh của y sẽ là NULL và y được coi như gốc mới của cây. Khi duyệt cây từ gốc sẽ gặp y chứ không gặp x. Thao tác thay thế nút được minh họa trong Hình 2.
Hình 2. Thao tác thay thế nút
Đây là 1 thao tác bậc thấp, tự nó có thể không hữu ích và có thể phá vỡ các ràng buộc, ví dụ tính chất tìm kiếm (xem mục 2), nhưng cần thiết để triển khai các thao tác lớn hơn, ví dụ thao tác xóa phần tử. Để tiện theo dõi trong Hình 2 đã lược bỏ các nút lá. Nếu thay nút 3 trong Hình 2a bằng nút 6 thì sẽ thu được cấu trúc liên kết như Hình 2b và nút 6 được coi như gốc mới của cây, nút 3 và toàn bộ nhánh trái của nó như bị lược bỏ khỏi cây. Nếu thay nút 2 trong Hình 2a bằng nút 1 thì sẽ thu được cấu trúc liên kết như Hình 2c, nút 2 như bị lược bỏ khỏi cây khi duyệt từ gốc.
Thao tác xoay làm hoán đổi vai trò của nút dưới và nút trên, khi áp dụng cho cây nhị phân tìm kiếm thì tính chất tìm kiếm vẫn được duy trì. Đây là thao tác cần thiết để triển khai các thao tác lớn hơn trong cây đỏ đen (xem mục 3). Thao tác xoay được minh họa trên Hình 3.
Biểu diễn giản lược của cây nhị phân được sử dụng trong Hình 3 - chỉ biểu diễn các nút trong, lược bỏ giá trị NULL và các chi tiết liên kết, giá trị của khóa được đặt trong hình chữ nhật, nút gốc được đặt cao hơn các nhánh của nó, nút trái nằm ở phía dưới và lệch sang bên trái, còn nút phải nằm ở bên phải. Các nhánh được biểu diễn trong hình tam giác. Liên kết đi lên nhưng không gắn với nút phía trên thể hiện nút có thể có nút trên hoặc không (nếu nó là gốc cây).
Hình 3. Thao tác xoay
Có 2 cách xoay đối xứng nhau, trong Hình 3a các nút có xu hướng dồn sang phía trái vì vậy được gọi là xoay trái, trong khi đó trong Hình 3b các nút có xu hướng dồn sang phải vì vậy được gọi là xoay phải. Để xoay trái thì nút được chọn làm mốc phải có nhánh phải, trong Hình 3a khi xoay trái tại 3 thì cấu trúc liên kết được điều chỉnh như sau: Nhánh trái của 5 được chuyển thành nhánh phải của 3, nút 3 được thay bằng nút 5, cuối cùng toàn bộ nhánh có gốc là 3 được thiết lập như nhánh trái của 5. Để xoay phải thì nút được chọn làm mốc phải có nhánh trái, trong Hình 3b để xoay phải tại 2 thì cấu trúc liên kết được điều chỉnh như sau: Nhánh phải của 1 được chuyển thành thánh trái của 2, nút 2 được thay bằng nút 1, cuối cùng toàn bộ nhánh có gốc là 2 được thiết lập như nhánh phải của nút 1.
Cây nhị phân tìm kiếm là cây nhị phân trong đó các nút của nó thỏa mãn tính chất tìm kiếm: Với x là 1 nút bất kỳ: Nếu y là nút trái của nó thì y.key <= x.key. Nếu z là nút phải của nó thì z.key >= x.key. Trong điều kiện không có trùng lặp khóa thì: y.key < x.key và z.key > x.key. Xem ví dụ trên Hình 4.
Hình 4. (a) - Cây nhị phân tìm kiếm;
(b) - Không thỏa mãn tính chất tìm kiếm.
Cây nhị phân trong Hình 4a có nút trái nhỏ hơn gốc và nút phải lớn hơn gốc, thỏa mãn tính chất tìm kiếm. Trong hình 4b, cả nút trái và nút phải đều nhỏ hơn gốc, vì vậy không phải cây nhị phân tìm kiếm.
Dựa trên tính chất tìm kiếm có thể tìm phần tử trong cây nhị phân tìm kiếm như sau:
B1. Nếu nút gốc là NULL - phần tử cần tìm không có trong cây thì kết thúc thao tác với kết quả NULL. Nếu ngược lại thì chuyển sang B2.
B2. So sánh khóa cần tìm với nút gốc, có 3 trường hợp:
1. Nếu bằng nhau thì nút gốc chính là nút cần tìm. Kết thúc tìm kiếm với kết quả là nút gốc hiện tại.
2. Nếu khóa cần tìm nhỏ hơn khóa của nút gốc hiện tại thì phần tử cần tìm chỉ có thể nằm trong nhánh trái. Các phần tử trong nhánh phải đều lớn hơn giá trị ở gốc, vì vậy nhánh phải không thể chứa phần tử cần tìm. Lặp lại từ B1 với nút gốc mới là nút trái của nút gốc hiện tại.
3. Nếu ngược lại - khóa cần tìm lớn hơn nút gốc thì phần tử cần tìm chỉ có thể nằm trong nhánh phải. Lặp lại từ B1 với nút gốc mới là nút phải của nút gốc hiện tại.
Các ví dụ tìm kiếm phần tử được cung cấp trong Hình 5.
Hình 5. Tìm phần tử trong cây nhị phân tìm kiếm
Thử tìm 6 trong Hình 5a, đầu tiên so sánh với gốc của cây, 6 > 5 do đó tiếp tục tìm trong nhánh phải, 6 < 7 do đó tiếp tục tìm trong nhánh trái, 6 = 6 tìm thấy phần tử sau 3 lần so sánh.
Tiếp tục thử tìm 7 trong hình 3b, các bước so sánh như sau: 7 > 1 - tìm trong nhánh phải, 7 > 3 - tìm trong nhánh phải, 7 > 5 - tìm trong nhánh phải, 7 = 7 tìm thấy phần tử sau 4 lần so sánh.
Độ phức tạp của thao tác tìm phần tử trong cây nhị phân tìm kiếm trong trường hợp xấu nhất phụ thuộc vào độ cao của cây. Trong hình 5a là 1 cây nhị phân tìm kiếm cân bằng với 7 phần tử, có thể tìm 1 phần tử bất kỳ với không quá 3 lượt so sánh. Trong khi đó, cây nhị phân tìm kiếm trong hình 5b có 4 phần tử lệch hoàn toàn về 1 phía, trong trường hợp xấu nhất tìm 1 phần tử cần tới 4 lượt so sánh. Trong trường hợp tổng quát, độ phức tạp của thao tác tìm kiếm trên cây nhị phân tìm kiếm với n phần tử là O(n).
Trong điều kiện chỉ cần duy trì tính chất tìm kiếm có thể thêm phần tử vào cây nhị phân tìm kiếm bằng 1 giải thuật đơn giản: Trước tiên thực hiện xử lý giống như tìm kiếm phần tử trong cây. Nếu phần tử cần thêm vào đã có trong cây thì thực hiện các xử lý cần thiết tùy theo trường hợp ứng dụng, thường có thể đưa ra cảnh báo và kết thúc thao tác, hoặc có thể cập nhật giá trị gắn với khóa, v.v.. Nếu phần tử cần thêm vào là phần tử mới thì tiến trình tìm kiếm sẽ dẫn đến 1 nút lá và có thể đặt phần tử mới vào vị trí đó mà vẫn bảo toàn tính chất tìm kiếm. Giải thuật cụ thể như sau, bắt đầu từ gốc cây:
B1. Nếu nút gốc hiện tại là NULL, thì thay thế nó bằng phần tử cần được thêm vào. Nếu ngược lại thì chuyển sang B2.
B2. So sánh phần tử cần được thêm vào với gốc hiện tại. Có 3 trường hợp:
1. Nếu phần tử = gốc, phần tử đã có trong cây thì thực hiện các xử lý cần thiết tùy theo trường hợp ứng dụng sau đó kết thúc thao tác.
2. Nếu phần tử < gốc thì lặp từ B1 với gốc mới là nút trái của gốc hiện tại.
3. Nếu phần tử > gốc thì lặp từ B1 với gốc mới là nút phải của gốc hiện tại.
Các ví dụ minh họa thêm phần tử vào cây nhị phân tìm kiếm được cung cấp trong Hình 6.
Hình 6. Thêm phần tử vào cây nhị phân tìm kiếm
Trong Hình 6a, ở trạng thái bắt đầu phần tử đầu tiên được thêm vào thành gốc của cây. Tiếp theo trong Hình 6b, 3 < 5 và nút trái của 5 là NULL, vì vậy 3 được thêm vào bên trái 5, trong Hình 6c, 8 được thêm vào bên phải 5. Trong Hình 6d, 6 > 5 và 5 có nhánh phải, vì vậy di chuyển sang nhánh phải, tiếp theo 6 < 8 và nút trái của 8 là NULL vì vậy 6 được thêm vào bên trái 8. Trong Hình 6e, 2 được thêm vào bên trái 3. Trong Hình 6f, 1 < 5 và 5 có nhánh trái, vì vậy di chuyển sang nhánh trái, sau đó 1 < 3 và 3 cũng có nhánh trái vì vậy tiếp tục di chuyển sang nhánh trái, cuối cùng 1 < 2 và nút trái của 2 là NULL, vì vậy 1 được thêm vào bên trái 2.
Giải thuật thêm phần tử vào cây nhị phân tìm kiếm trong mục này có thể dẫn đến cấu trúc cây lệch hẳn về 1 phía. Cây nhị phân tìm kiếm trong Hình 6f không thỏa mãn tính chất cân bằng, nhánh trái của nút 3 có chiều cao = 2 còn nhánh phải có chiều cao = 0. Nếu tiếp tục thêm các phần tử < 1 theo thứ tự giảm dần thì sẽ thu được 1 cây nhị phân tìm kiếm lệch hẳn về phía trái.
Để xóa phần tử trước tiên cần tìm kiếm phần tử trong cây, sau đó điều chỉnh cấu trúc liên kết để tách nút tìm được khỏi cây, rồi cuối cùng thực hiện các thao tác giải phóng bộ nhớ cần thiết. Vấn đề tìm kiếm phần tử đã được trình bày trong mục 2.2. Vấn đề giải phóng bộ nhớ thường phụ thuộc vào triển khai cụ thể, vì vậy tạm thời chưa được đề cập tới trong mục này. Còn thao tác tách rời nút khỏi cây mà vẫn duy trì tính chất tìm kiếm về cơ bản có 3 trường hợp có khác biệt về cách xử lý. Trường hợp đầu tiên cũng là trường hợp đơn giản nhất, nếu cả 2 nút dưới của nút cần xóa đều là các nút lá thì chỉ cần cắt liên kết từ nút trên (nếu có) để tách nó khỏi cây. Nếu nút cần xóa là gốc của cây thì cây sẽ rỗng sau khi xóa.
Trường hợp 2 có thể được tách thành 2 trường hợp đối xứng, nếu nút cần xóa chỉ có 1 nhánh (có thể là nhánh trái hoặc nhánh phải) thì thay thế nó bằng nút dưới. Các ví dụ minh họa cho trường hợp xóa nút 1 nhánh được cung cấp trong Hình 7.
Hình 7. Xóa nút 1 nhánh
Nút 5 trong Hình 7a chỉ có 1 nhánh trái và là nút trái của nút trên, nút 5 được tách khỏi cây bằng cách liên kết nút 2 (nút dưới) với nút 6 (nút trên) theo liên kết trái của nút trên. Tương tự nút 7 trong Hình 7b chỉ có 1 nhánh phải, để tách phần tử 7 trước tiên cần thay nó bằng nút 9, kết quả là cấu trúc như trong Hình 7c. Trong Hình 7 sau khi thay thế 1 nút bằng 1 nút khác, nút bị thay thế (nút 5 và nút 7) vẫn chứa liên kết tới đỉnh của nó, tuy nhiên để tập trung vào cấu trúc cây sau khi xóa, các liên kết đó đã được lược khỏi hình vẽ.
Trường hợp 3 là trường hợp phức tạp nhất, nếu nút cần xóa có 2 nhánh thì có 2 lựa chọn đối xứng nhau để tách nó khỏi cây - có thể thay thế nút cần xóa bằng nút liền trước hoặc nút liền sau. Theo phương án sử dụng nút liền sau cần xử lý 3 nhóm liên kết: 1) Liên kết với nhánh phải, nếu nút liền sau của nút cần xóa là nút phải của có thì có thể bỏ qua bước này. Nếu ngược lại, nút liền sau nằm trong nhánh trái của nút phải của nút cần xóa thì chuyển nhánh phải của nút liền sau thành nhánh trái của nút trên của nút liền sau và chuyển nhánh phải của nút cần xóa thành nhánh phải của nút liền sau; 2) Chuyển nhánh trái của nó thành nhánh trái của nút liền sau. Nút cần xóa có nhánh phải vì vậy nút liền sau của nó phải nằm trong nhánh phải với nút trái là nút lá; 3) Thiết lập liên kết với nút trên, thay thế nút cần xóa bằng nút liền sau của nó. Các ví dụ minh họa thao tác xóa nút với 2 nhánh được cung cấp trong Hình 8.
Hình 8. Xóa nút có 2 nhánh
Thử xóa nút 5 trong Hình 8a, nút tiếp theo của 5 là 7, nút 7 không có nhánh trái. Để tách nút 5 khỏi cây trước tiên cần chuyển nhánh trái của nó thành nhánh trái của nút 7, sau đó thay thế nút 5 bằng nút 7. Thử xóa nút 6 trong Hình 8b, nút tiếp theo của nút 6 là nút 8 - nút trái nhất trong nhánh phải của nút 6. Để tách nút 6 khỏi cây trước tiên cần thay thế nút 8 bằng nút phải của nó (chuyển nhánh y thành nhánh trái của 9), sau đó chuyển nhánh phải của 6 thành nhánh phải của 8, chuyển nhánh trái của nút 6 thành nhánh trái của nút 8, rồi cuối cùng thay thế nút 6 bằng nút 8. Tính chất tìm kiếm được bảo toàn sau khi thay đổi các liên kết.
Cây đỏ đen là 1 loại cây nhị phân tìm kiếm thỏa mãn các ràng buộc sau:
1) Mỗi nút chỉ có thể được tô mầu đỏ hoặc đen.
2) Nút gốc là nút đen.
3) Tất cả lá đều là các nút đen.
4) Cả 2 nút dưới của nút đỏ đều là các nút đen
5) Tất cả các đường đi đơn giản từ gốc tới lá đều có cùng số lượng nút đen.
Tính chất 5 có thể được diễn đạt theo cách khác nhưng tương đương: “Đối với 1 nút trong bất kỳ, tất cả các đường đi đơn giản từ nút đó tới lá đều có cùng số lượng nút đen”. Các ràng buộc đã liệt kê được gọi chung là các tính chất đỏ đen.
Số lượng nút đen trên đường đi đơn giản từ gốc tới lá, không đếm gốc được gọi là độ cao đen của cây đỏ đen, ký hiệu là bh (black height). Tính chất 5 đảm bảo độ cao đen là 1 đại lượng xác định.
Đồng thời các tính chất đỏ đen cũng đảm bảo: “Một cây đỏ đen với n nút trong có độ cao không quá 2 log(n + 1)”. Trong mục này cơ số 2 được sử dụng cho các hàm log.
Trước tiên chúng ta sẽ chứng minh 1 khẳng định tương đương “Cây đỏ đen có độ cao đen bh có tối tiểu 2bh - 1 nút trong”. Khẳng định này có thể được chứng minh bằng phương pháp quy nạp:
Với 1 cây đỏ đen có bh = 0, theo tính chất 2 thì cây như vậy chỉ có thể là cây rỗng, số lượng nút trong của nó = 0 = 20 - 1.
Với 1 cây đỏ đen có bh = 1, cũng theo tính chất 2 thì nó phải có nút gốc, vì vậy số lượng nút trong của nó >= 1, nghĩa là >= 21 - 1.
Với 1 cây đỏ đen có bh > 1 thì độ cao đen của các cây con là nhánh trái và nhánh phải của nó >= bh - 1. Vì vậy số lượng nút trong của nó >= 2 * (2bh - 1 - 1) + 1, nghĩa là >= 2bh - 1.
Như vậy đối với 1 cây đỏ đen có n nút trong thì độ cao đen tối đa của nó là log(n + 1). Đồng thời theo tính chất 4 thì số lượng nút trong của 1 đường đi đơn giản bất kỳ xuất phát từ gốc (nút đen) không vượt quá 2 * bh. Vì vậy có thể khẳng định chắc chắn độ cao (cực đại) của cây <= 2 log(n + 1).
Tính chất 4 đảm bảo với 1 nút trong bất kỳ trong cây đỏ đen thì chiều cao nhánh trái và chiều cao nhánh phải của nó chênh lệch nhau không quá 2 lần. Vì vậy cây đỏ đen được coi là cây nhị phân tìm kiếm gần cân bằng. Cùng với các thao tác thêm và xóa nút không quá phức tạp, tính chất gần cân bằng của cây đỏ đen đảm bảo khả năng tìm kiếm phần tử đủ nhanh với phân bố dữ liệu bất kỳ. Độ phức tạp của thao tác tìm kiếm trong cây đỏ đen n phần tử là O(log n). Cây đỏ đen là 1 lựa chọn tốt để quản lý dữ liệu trong bộ nhớ trong trường hợp cần có khả năng tìm kiếm nhanh. Trong thực tế cây đỏ đen là 1 cấu trúc dữ liệu quan trọng, được sử dụng phổ biến, các trường hợp ứng dụng tiêu biểu có thể kể đến như lõi của hệ điều hành Linux, trong nhiều triển khai ánh xạ khóa-giá trị, v.v..
Các ví dụ minh họa khái niệm cây đỏ-đen được cung cấp trong Hình 9.
Hình 9. Các tính chất đỏ đen
Giá trị NULL trong triển khai có thể được xác định dựa trên quy ước, không phải 1 nút hoàn chỉnh, không được cấp phát bộ nhớ để lưu các thuộc tính. Vì vậy tính chất 3 - Lá là nút đen - có thể được coi như được duy trì dựa trên quy ước. Trong Hình 9a là 1 cây đỏ đen đơn giản với bh = 1. Cây trong Hình 9b vi phạm tính chất 1 bởi vì nút 3 có màu xanh (sẽ chỉ liệt kê các tính chất bị vi phạm), nhưng mỗi nút chỉ có thể là đỏ hoặc đen. Cây trong Hình 9c vi phạm tính chất 2 bởi vì nút 1 là nút đỏ, nhưng nút gốc phải là nút đen. Cây trong Hình 9d vi phạm tính chất 4, nút 3 là nút dưới của nút 5, cả 2 đều là các nút đỏ, tuy nhiên các nút dưới của nút đỏ phải là các nút đen. Cây trong Hình 9e vi phạm tính chất 5, đường đi tới lá từ nút 1 (gốc) qua nhánh trái chứa 1 nút đen (đếm lá nhưng không đếm gốc), còn đường đi qua nhánh phải chứa 2 nút đen. Tuy nhiên theo tính chất 5 thì tất cả các đường đi đơn giản từ gốc tới lá phải có cùng số lượng nút đen.
Thao tác thêm phần tử vào cây đỏ đen trước tiên được xử lý như thêm vào cây nhị phân tìm kiếm, nút mới đầu tiên được tô mầu đỏ, sau đó các hiệu chỉnh cần thiết được thực hiện để khôi phục các tính chất đỏ đen bị vi phạm.
Nút mới được thêm vào là nút đỏ vì vậy các tính chất 1 - mỗi nút chỉ có thể là đỏ hoặc đen, tính chất 3 - lá là nút đen, tính chất 5 - tất cả đường đi đơn giản từ 1 gốc tới lá đều có cùng số lượng nút đen không bị ảnh hưởng. Tính chất 2 - gốc cây là nút đen có thể bị phá vỡ nếu cây rỗng trước khi thêm nút mới, tuy nhiên có thể được khôi phục ngay bằng cách điều chỉnh mầu của nút gốc thành đen. Tính chất 4 - các nút dưới của nút đỏ là các nút đen có thể bị phá vỡ nếu nút mới được thêm vào dưới nút đỏ. Có thể khái quát vấn đề khôi phục tính chất đỏ đen từ trạng thái như vậy thành vấn đề khôi phục tính chất đỏ đen của 1 cây với 1 nút đỏ có nút dưới là nút đỏ, ngoài ra không có bất kỳ vi phạm nào khác. Các nút đỏ trong đoạn vi phạm theo vai trò lần lượt được gọi là nút đỏ dưới và nút đỏ trên.
Có 2 trường hợp lớn khác nhau nhưng đối xứng: Trường hợp nút đỏ trên là nút trái trong liên kết với nút trên của nó được minh họa trong Hình 10 (t là nút trái của tt). Còn trường hợp nút đỏ trên là nút phải trong liên kết với nút trên của có được xử lý hoàn toàn tương tự, chỉ cần thay thao tác xoay phải thành xoay trái, liên kết trái thành liên kết phải, và ngược lại, v.v.. vì vậy được để lại để bạn đọc tự phân tích thêm.
Trong Hình 10 nút đỏ dưới được ký hiệu là n, nút đỏ trên được ký hiệu là t, nút trên của t được ký hiệu là tt, nút cạnh t (nút dưới còn lại của tt) được ký hiệu là s, nhãn của nút đỏ được viết thường, còn nhãn của nút đen được viết hoa. Trong mỗi ví dụ ở trạng thái bắt đầu của mỗi lượt xử lý tính chất đỏ đen chỉ bị vi phạm ở đoạn t-n (2 nút đỏ liên tiếp). Trong lượt xử lý đầu tiên n là nút mới được thêm vào cả 2 nút dưới của n đều là lá, nhưng trong các bước lặp tiếp theo khi các nút đỏ vi phạm đã được đẩy lên cao hơn thì n có thể có các nhánh dưới. Tổng hợp lại có thể coi các nhánh trong Hình 10 là không bắt buộc, nhưng được biểu diễn đầy đủ để tiện theo dõi. Bên cạnh đó tính chất đỏ đen chỉ bị vi phạm ở đoạn t-n, vì vậy t phải có nút trên TT là nút đen.
Hình 10. Khắc phục vấn đề 2 nút đỏ liên tiếp
Như trong Hình 10a nếu nút cạnh t (nút s) là nút đỏ, thì tô lại mầu các nút t và s thành đen, còn nút TT thành đỏ. Sau khi tô lại mầu có thể xảy ra 3 trường hợp: 1) Nếu TT là gốc cây thì vi phạm tính chất 2 - gốc cây là nút đen, có thể được sửa bằng cách tô lại TT thành đen. Các tính chất đỏ đen được đáp ứng sau đó; 2) Nếu tt có đỉnh đen thì các tính chất đỏ đen cũng đã được thỏa mãn; 3) Nếu tt có đỉnh đỏ thì tính chất 4 bị vi phạm ở đoạn tt và đỉnh của có, vì vậy lặp lại thao tác với tt là n mới. Các xử lý cho trường hợp trong Hình 10a không phụ thuộc vào n là nút trái hay nút phải của t.
Theo tính chất 1 - mỗi nút chỉ có thể là đỏ hoặc đen, Hình 10b minh họa trường hợp còn lại. Nếu cạnh t là nút đen thì tô lại mầu của t thành đen, và mầu của TT thành đỏ. Sau đó cần đảm bảo n là nút dưới trái của t - nếu nó là nút dưới phải thì xoay trái tại t, sau đó hoán đổi vai trò của t và n và tiếp tục xử lý như n là nút dưới trái của t. Cuối cùng thực hiện xoay phải tại tt. Các tính chất đỏ đen được đảm bảo sau đó.
Tính chất bất biến “Ở trạng thái bắt đầu của mỗi lượt xử lý tính chất đỏ đen chỉ bị vi phạm ở đoạn t-n (2 nút đỏ liên tiếp)” có thể được chứng minh như sau: Có thể thấy các tính chất 1, 2 và 3 luôn được đảm bảo. Còn lại việc đảm bảo tính chất 5 qua các bước xử lý có thể được chứng minh như sau: Đặt u, v, w, x, y lần lượt là số lượng nút đen trên các đường đi từ gốc tới lá của các nhánh với nhãn tương ứng (đếm cả gốc của nhánh, = bh + 1 nếu gốc là nút đen). Đối với trường hợp trong Hình 10a, tính chất 5 được đáp ứng ở trạng thái bắt đầu vì vậy u = v = w = x = y. Sau khi tô lại mầu thì số lượng nút đen trên các đường đi đơn giản từ tt qua các nhánh tới là là u + 1 = v + 1 = w + 1 = x +1 = y + 1. Số lượng nút đen trong các đường đi đơn giản đến lá đều bằng nhau, tính chất 5 được đảm bảo.
Đối với trường hợp trong Hình 10b, tính chất 5 được đảm bảo ở trạng thái bắt đầu vì vậy u = v = w, x = y và u = x + 1. Ở trạng thái kết thúc số lượng nút đen trong các đường đi đơn giản từ T tới lá qua các nhánh đều bằng nhau, không thay đổi so với trạng thái ban đầu, tính chất 5 được đảm bảo.
Sau mỗi bước lặp, nếu các tính chất đỏ đen chưa được đáp ứng thì cũng chỉ có tính chất 4 - nút dưới của nút đỏ phải là nút đen bị vi phạm với với đoạn vi phạm bị đẩy lên cao hơn 2 mức về phía nút gốc. Nếu cứ tiếp tục lặp thì sau 1 số bước hữu hạn TT phải là gốc cây hoặc đỉnh của TT là gốc cây, vì vậy các xử lý luôn đảm bảo các tính chất đỏ đen được khôi phục sau 1 số bước hữu hạn.
Thao tác xóa phần tử khỏi cây đỏ đen được thực hiện qua 2 bước: Bước 1 xóa phần tử như với cây nhị phân tìm kiếm; Bước 2 khôi phục các tính chất đỏ đen nếu bị vi phạm. Các trường hợp phá vỡ tính chất đỏ đen được minh họa trong Hình 11.
Trường hợp nút bị xóa không có nút dưới được minh họa trong Hình 11a. Nếu nút bị xóa là nút đen (ký hiệu là D) và có đỉnh (ký hiệu là (t) - có thể là đỏ hoặc đen) thì sau khi xóa đường đi qua (t) và vị trí cũ của D bị giảm 1 nút đen, vì vậy tính chất 5 bị phá vỡ. Nếu D không có đỉnh (D là gốc cây), hoặc nút bị xóa là nút đỏ thì các tính chất đỏ đen vẫn được bảo toàn sau khi xóa.
Trường hợp nút bị xóa có đúng 1 nhánh thì nó phải là nút đen và chỉ có thể có 1 nút dưới là nút đỏ được minh họa như trong Hình 11b. Nút đỏ dưới được ký hiệu là b, có thể là nút trái hoặc nút phải, tuy nhiên cách xử lý tương tự. Sau khi xóa D và tô lại mầu của b thành đen thì các tính chất đỏ đen được đảm bảo.
Hình 11. Các trường hợp cần cân bằng sau khi xóa nút
Các trường hợp d có 2 nhánh dưới được minh họa trong Hình 11c và Hình 11d, mầu của d không ảnh hưởng tới các xử lý. Trong ví dụ 1 trong Hình 11c, nút dưới của bị xóa là nút đỏ vì vậy D phải là nút đen. Trong các ví dụ còn lại trong Hình 11c và Hình 11d mầu của nút bị xóa không xác định, có thể là đỏ hoặc đen. Nếu trước khi xóa s có mầu đỏ thì các tính chất đỏ đen được bảo toàn sau khi xóa và tô lại mầu trực tiếp. Nếu ngược lại, s có mầu đen thì đường đi từ đỉnh của s qua vị trí cũ của s bị giảm đi 1 nút đen, tính chất 5 bị phá vỡ ngay sau khi xóa.
Trường hợp nút tiếp theo của (d) là nút dưới phải của nó được minh họa trong Hình 11c. Nếu S là nút đen thì chỉ có thể xảy ra 2 trường hợp: 1) Nếu S có nút dưới phải là nút đỏ, ký hiệu là nút r, sau khi xóa D và tô lại mầu r thành đen thì các tính chất đỏ đen được bảo toàn; 2) Nếu S có 2 nút lá thì sau khi xóa tính chất 5 bị vi phạm, số lượng nút đen trong đường đi qua (s) về phía nút lá ít hơn 1 so với các đường đi khác.
Trường hợp nút tiếp theo là nút trái nhất của nhánh phải được minh họa trong Hình 11d. Nếu nút tiếp theo là nút đỏ thì sau khi xóa (d) và tô lại mầu s thành mầu cũ của (d) thì các tính chất đỏ đen được bảo toàn. Nếu nút tiếp theo là nút đen thì có 2 trường hợp tương tự như trong Hình 11c, nếu S có nút dưới phải đỏ, ký hiệu là r, thì sau khi xóa (d) và tô lại mầu S thành mầu cũ của (d), tô r thành mầu đen thì các tính chất đỏ đen được bảo toàn. Nếu S có 2 nút lá thì sau khi xóa và tô lại mầu thì tính chất 5 bị vi phạm, đường đi qua T về phía nút lá ở phía trái bị giảm 1 nút đen.
Sau khi xóa nút và hiệu chỉnh mầu trực tiếp chỉ có tính chất 5 có thể bị vi phạm ở 1 nút duy nhất có 1 nút dưới là nút lá, nhánh còn lại có bh = 1. Trong Hình 11a nút (t) có nút lá bên trái. Trong Hình 11c là nút (s) có nút lá bên phải. Trong Hình 11d nút T có nút lá bên trái.
Thao tác khôi phục tính chất đỏ đen có thể được thực hiện qua nhiều lượt, trước khi bắt đầu vòng lặp tính chất 5 chỉ bị vi phạm ở 1 đoạn duy nhất có 1 nút dưới là nút đen mà đường đi qua đó có ít hơn 1 nút đen so với đường đi qua nhánh còn lại. Ngay sau khi xóa nút và hiệu chỉnh mầu trực tiếp nút đen dưới ở đoạn vi phạm là nút lá. Sau mỗi bước lặp vị trí nút vi phạm được nâng lên cao hơn về phía gốc cây. Thao tác khôi phục tính chất đỏ đen từ trạng thái vi phạm tính chất 5 như mô tả có thể được chia thành 2 trường hợp lớn khác nhau nhưng đối xứng: 1) Nút đen là nút dưới trái; 2) Nút đen là nút dưới phải. Các xử lý cho trường hợp nút đen là nút dưới trái được minh họa trong Hình 12. Trường hợp nút dưới phải đen được khắc phục tương tự, thay xoay trái thành xoay phải, và ngược lại v.v.. vì vậy được để lại để bạn đọc tự phân tích thêm.
Nếu nút cạnh N (nút dưới còn lại của T) là nút đỏ (nút s) như trong Hình 12a (s đỏ thì T phải là nút đen), thì xoay trái tại T rồi tô lại T thành đỏ và s thành đen. Tính chất 5 vẫn bị vi phạm ở đoạn t-N, tuy nhiên nút cạnh N đã là nút đen. Trong các trường hợp tiếp theo cả N và S đều là các nút đen.
Trường hợp cả 2 nút dưới của S đều là các nút đen được minh họa trong Hình 12b, tiếp theo nếu đỉnh của N (nút t) là nút đỏ thì tô lại mầu t thành đen và S thành đỏ, số lượng nút đen trên đường đi qua T và N được tăng lên 1, và được giữ nguyên trên đường đi qua s vì vậy các tính chất đỏ đen đã được đảm bảo. Trong trường hợp còn lại trong Hình 12b, nếu đỉnh của N là nút đen thì tô lại mầu S thành đỏ, đường đi qua s sẽ giảm 1 nút đen, vì vậy tất cả các đường đi đơn giản từ T tới lá đều có cùng số lượng nút đen. Sau khi tô lại s thành đỏ nếu T là gốc cây thì tính chất đỏ đen đã được đảm bảo, nếu ngược lại thì tính chất 5 bị vi phạm ở nút T, số lượng nút đen trên đường đi từ gốc cây qua T tới lá sẽ ít hơn 1 so với các đường đi khác không qua T. Vì vậy lặp lại các xử lý với T là N mới trong trường hợp này.
Trường hợp trong các nút dưới của S có nút đỏ được minh họa trong Hình 12c và Hình 12d. Trong Hình 12c nếu nút dưới của S ở phía gần N (nút cn) là nút đỏ và nút dưới của S ở phía xa N (nút DN) là nút đen thì thực hiện xoay phải ở S rồi sau đó xoay trái ở (t) và tô lại mầu của cn là mầu cũ của (t). Các tính chất đỏ đen đã được đáp ứng sau đó.
Hình 12. Các trường hợp khôi phục độ cao đen
Như trong Hình 12d, (cn) có thể có mầu bất kỳ, mầu của (cn) không ảnh hưởng tới các xử lý vì vậy nút (cn) được giản lược khỏi hình vẽ, thực tế (cn) là gốc của nhánh x. Nếu dn là nút đỏ thì xoay trái tại (t) sau đó tô lại mầu S thành mầu cũ của (t), tô (t) thành mầu đen và dn thành mầu đen. Các tính chất đỏ đen đã được thỏa mãn sau đó.
Sự khôi phục tính chất 5 có thể được chứng minh tương đối đơn giản và tương tự cho các trường hợp. Đối với trường hợp trong Hình 12d, đặt u, v, x, y, z lần lượt là số lượng nút đen trong các đường đi đơn giản từ gốc của các nhánh tương ứng, có đếm cả nút gốc (= bh + 1 nếu gốc là nút đen). Do ở trạng thái bắt đầu xử lý tính chất 5 chỉ bị vi phạm ở đoạn (t)-N với 1 nút đen ít hơn, vì vậy u = v, x = y = z và x = u + 1. Sau khi xoay và tô lại mầu, số lượng nút đen từ (s) qua các nhánh (không đếm (s)) lần lượt là u + 2 = v + 2 = x + 1 = y + 1 = z + 1, chứng tỏ tính chất 5 đã được khôi phục.
Các xử lý chỉ được lặp lại trong trường hợp cả T, N, S, CN, DN đều là các nút đen và T không phải gốc cây. Tuy nhiên ở bước lặp tiếp theo cả N và T đều bị đẩy lên cao hơn 1 mức về phía gốc, vì vậy tiến trình xử lý sẽ luôn dừng sau 1 số bước hữu hạn, các tính chất đỏ đen luôn được khôi phục sau đó.
Tham khảo: https://github.com/bangoc/cgen
[1] Nhiều tài liệu khác gọi là nút cha - nút con.